Но практическая жизнь часто требует верно оценить шансы. И тут здравый смысл нередко подводит нас. Вот вам задача, известная как «проблема Монти Холла» — и ее решение, противоречащее здравому смыслу, но подтверждаемое математическим моделированием.

Представьте, что вы участвуете в игровом шоу, и вам предоставляется выбор из трех дверей. За одной дверью — новенькая машина; за двумя другими — козы. Игра заключается в простом выборе двери: что бы ни было за ней, вы выигрываете это. Козы, конечно, прекрасные животные. Но вам нужна машина.
Вы выбираете дверь номер один, но ведущий неожиданно говорит вам: «Вы бы передумали, если бы я сказал, что машина не за третьей дверью?».
Отлично, просто отлично! Ваши шансы резко выросли. Как их использовать наилучшим образом? При этом, речь идет именно о шансах: машина может быть и за первой дверью, и за второй. Менять или не менять уже принятое решение?
Здравый смысл говорит нам, что при выборе из двух дверей шансы угадать – 50%. То же говорит и теория вероятностей, если бы мы выбирали из двух с самого начала. Но наш задача сложнее – распределение вероятностей изменилось по ходу угадывания. Итак, дверь 1 или дверь 2?
Этот мысленный эксперимент называется проблемой Монти Холла, и на протяжении многих лет вызвал немало споров в математическом мире. Первоначально он был опубликован как письмо к редактору в выпуске журнала American Statistician за 1975 год, но по-настоящему стал популярен в 1990 году, когда колумнистка журнала Parade Мэрилин Вос Савант предложила его читателям своей колонки «Спросите Мэрилин».
Вы уже решили, стоит ли вам переходить на вторую дверь? Если вы хотите получить максимальные шансы на получение машине, сделайте это.
Вас смущает такая идея? Вы в хорошей компании. Когда Мэрилин дала такой совет в своей колонке, десятки тысяч читателей, в том числе около несколько тысяч профессиональных математиков, указали ей на ее неправоту. Пол Эрдёш, один из самых известных математиков XX века, работавший, в том числе и в области теории вероятностей, годами отказывался принимать этот результат, и сдался только тогда, когда его усадили перед компьютерным симулятором. В итоге, Эрдёш был вынужден согласиться с выводом Мэрилин, хотя ему это очень не понравилось.
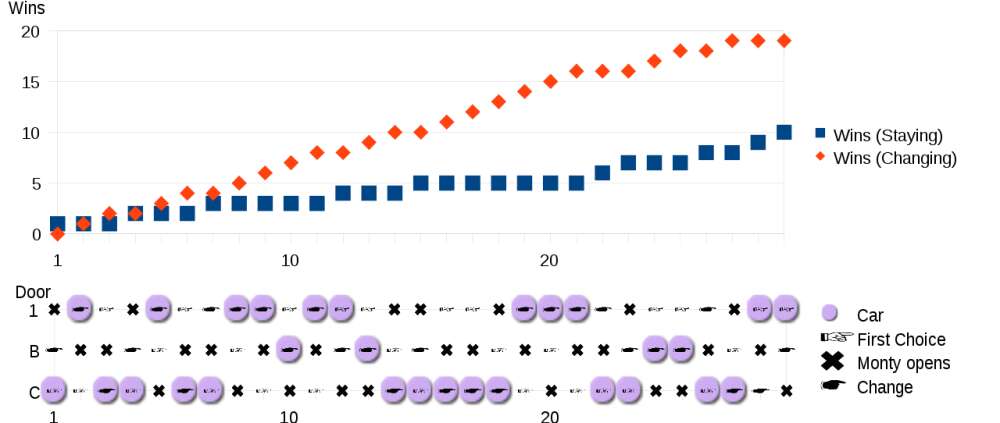
Но это действительно работает: поменяйте двери местами, и вы удвоите свои шансы на получение машины. Давайте посмотрим, почему.
В начале раунда у вас нет дополнительной информации. У всех трех дверей одинаковая вероятность того, что за ними будет стоять машина: 1/3.

Итак, ваша дверь, первая дверь, дает вам один шанс из трех выиграть эту машину, и есть два из трех шансов, что машина находится за дверьми номер два и три.
Но потом все меняется, потому, что вам дают новую информацию: машина не за третьей дверью. Предлагая вам возможность переключиться на вторую дверь, ведущий игрового шоу предлагает вам выбор между первой дверью и двумя другими, вместе взятыми — просто теперь вы знаете, что вероятность того, что машина находится за третьей дверью, равна нулю. Таким образом, у двери номер два есть две трети шансов скрывать за собой автомобиль.

Другими словами, первая дверь дает вам одну треть шансов на победу, а вторая дверь дает вам две трети шансов. Меняя двери, вы удваиваете свои шансы. Ваш здравый смысл бунтует? Наш тоже. Попробуем ему помочь.
Представим, что в этом игровом шоу миллион дверей вместо трех. За одной из дверей стоит машина, за остальными 999 999 — козы.

Вы снова выбираете дверь номер один, и ведущий снова дает вам новую информацию.
«За дверями с третьей по миллионную сидят козы, — говорит он вам. — Это меняет ваш выбор?»
Итак, ваш выбор теперь — первая дверь, которую вы выбрали из миллиона дверей, скрывающих 999 999 коз и единственную машину, или дверь номер два, которая остается единственной после локализации 999 998 коз. Если подумать об этом так, можно сделать результат немного более интуитивным: есть шанс один из миллиона, что первая дверь была правильным выбором, и поэтому единственная другая дверь, оставшаяся в игровом шоу, должна иметь шанс 999999 из 1000000 на победу.
Причина неинтуитивного ответа — нечто, называемое «условной вероятностью», и мы можем увидеть это нечто, используя правило вероятности, известное как теорема Байеса.
В математических обозначениях теорема Байеса выглядит так:

На словах это звучит как «вероятность возникновения события A при условии, что событие B происходит, равна вероятности возникновения события B при условии, что событие A происходит, умноженной на общую вероятность возникновения A, деленную на общую вероятность возникновения B».
Вот как это работает на конкретном примере. Представьте себе, что у вас есть сумка с тремя красными и двумя зелеными шарами. Вероятность выбрать вслепую красный шар составляет три из пяти — 60 процентов, а вероятность выбрать зеленый шар — два из пяти, или 40 процентов.

Но если вы уже выбрали красный шар, эти вероятности меняются. Количество шаров уменьшилось с пяти до четырех, два красных и два зеленых, и шансы выбрать шар любого цвета равны. С другой стороны, если вы уже выбрали зеленый шар, шанс выбрать зеленый при следующем подходе снижается до одного из четырех, а шанс выбрать красный шар становится равным трем четвертям.
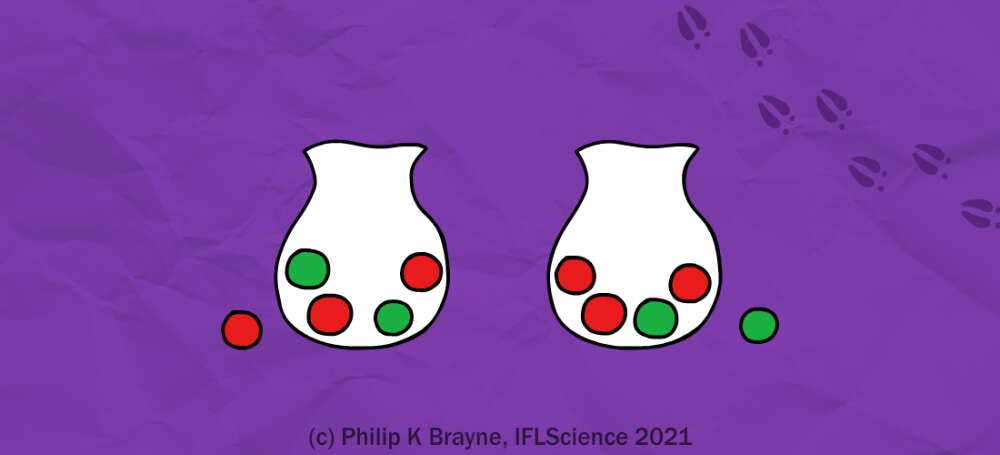
Если мы назовем событие A «взятием зеленого шара», а событие B «взятием красного шара», мы получим в точности теорему Байеса.

Итак, давайте воспользуемся теоремой Байеса для решения проблемы Монти Холла. Для наглядности предположим, что ведущий, заглянув за дверь, молча открыл ее — и там оказалась коза.
Понятно, что будь за дверью машина, ведущий бы ее не открыл. Потому, что шоу с угадыванием в этом случае утратило бы всякий смысл. То есть, вероятность того, что, заглянув за дверь ведущий откроет ее и облегчит нам задачу составляет ½. Машина или коза. Речь уже не о шансах наткнуться на козу, а о возможных действиях ведущего. Это другой вероятностный ряд.
Далее, мы будем называть открытие двери, скрывающей машину, «событием C», а двери, скрывающей козу, «событием G». Тогда для трех дверей соотношение вероятностей с учетом теоремы Байеса выглядит так:

P (C) — вероятность того, что машина находится за первой дверью, 1/3.
P (G) – вероятность того, что ведущий откроет нам третью дверь (оказавшись перед выбором «коза – открываю, машина – не открываю»), ½.
P (C | G) — вероятность того, что машина окажется за первой дверью после того, как ведущий открыл третью дверь. Она не изменилась по сравнению с P (C), и составляет все ту же 1/3. Это означает, что вероятность того, что машина окажется за другой дверью, P (-C), должна составлять две трети, поскольку сумма вероятностей равна 1. Но в данный момент единственная другая дверь, за которой может находиться машина — это вторая дверь.
Наш здравый смысл бунтует – но математика не врет, и это подтверждается экспериментально.
Проблема Монти Холла — не единственная игра, в которой условная вероятность приводит к запутанным результатам. Еще более спорным является правильный ответ на «парадокс мальчика и девочки» или «проблему двух детей», которая гласит:
У мистера Смита двое детей. Один из них — мальчик. Какова вероятность того, что оба мальчики?
Мы дадим вам минутку подумать.
Если вы сказали 50%, или ½, или один из двух, или что-то подобное, то с математической точки зрения это неверно. Правильный ответ — 1/3.

Тем не менее, никто из тех, кто сказал ½ не должен обижаться на это: очень умные люди привели немало убедительных аргументов в пользу того, что правильный ответ все же таков.
Подводя итог: условная вероятность — это боль, и, если вы ее не совсем понимаете, вы в хорошей компании.
В Галактике может быть множество мертвых цивилизаций, уничтоженных собственной наукой и технологиями. Новое исследование NASA оценило вероятность встречи с внеземными цивилизациями.
По материалам IFLScience
Читайте также:
Астероид Апофис: астрономы уточнили вероятность столкновения с Землей
Кофе снижает вероятность старческого слабоумия





